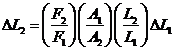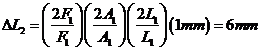VARIATION PROBLEMS:
In your Algebra class, you discussed the two types of variation: a direct proportion and an inverse proportion. A third type is when a variable say, z, varies directly with the product of two variables x and y, that is
![]()
Where k is the constant of proportionality between z and the product xy. The variable z is said to vary jointly with x and y. One good example of joint variation is momentum. The momentum of an object varies directly with the product of its mass and velocity (k = 1).
![]()
EXAMPLE 1:
The kinetic energy of a body KE is given by the equation
![]()
Where m represents the mass of the object and v, its velocity. The equation, tells us that KE varies directly with the product of m and v2 where the constant of proportionality k = 1/2. Suppose a car of mass mA, acquires a kinetic energy KEA of 10,000 J when it moves at a velocity vA . What will be the kinetic energy of a second car that is twice as heavy and twice as fast as the first car?
SOLUTION:
The equation above can also be written as (following the technique suggested in “USING PROPORTION”),
![]()
This suggests that,
![]()
Solving for KEB,
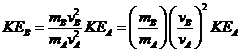
Substituting ![]() and
and ![]() ,
,
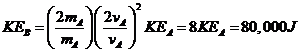
In many instances, direct, inverse and joint variation are combined. We then have a compound variation. A good example of such a compound variation is the dependence of centripetal force on the mass, velocity and radius of the circle of revolution. The centripetal force is given by the expression
![]() Equation (1)
Equation (1)
Or the
centripetal force varies directly with the mass, with the square of the
velocity, and it varies inversely with the radius of revolution. Since the
velocity v is equal to
![]() , where T is the period of revolution, we can write the Equation
(1) as
, where T is the period of revolution, we can write the Equation
(1) as
![]() Equation (2)
Equation (2)
Equation (2) shows that for a
given body, the centripetal force varies directly with the radius of revolution
and inversely with the square of the period. The question that arises is why
the centripetal force
varies inversely with R in Equation (1) but that
varies directly with R in Equation (2). We should, however, bear in mind what other
quantities are implied as being
constant. In (1) ,
![]() for a given body
moving with constant speed, while in (2) ,
for a given body
moving with constant speed, while in (2) , ![]() for a body whose
period of rotation is kept constant.
for a body whose
period of rotation is kept constant.
EXAMPLE 2:
A stone is whirled in a horizontal circle by means of a string 50 cm long and with a period of 0.50 s. If the tension in the string is 20 N, what is the tension if the string is shortened to 25 cm and the period is also shortened to 0.25 s? (Note: the tension in the string provides the centripetal force for the stone to follow a circular trajectory)
SOLUTION:
It is implied in the problem that
![]()
Where ![]()
Rearranging the equation so that the constant k is on one side and the variables are on the other ,
![]() (equation A)
(equation A)
If we let the new tension new radius and the new period be ![]() ,
, ![]() , respectively, Equation A, gives us
, respectively, Equation A, gives us
![]()
Solving for ![]() ,
,
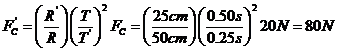
EXAMPLE 3:
Hooke’s Law states that within the elastic limit, the
stress ![]() is proportional to strain
is proportional to strain ![]() . The constant of proportionality is known
as Young’s modulus of elasticity, Y.
In equation
. The constant of proportionality is known
as Young’s modulus of elasticity, Y.
In equation
![]()
A steel wire of length L, of cross-sectional area A is subjected to a tension T. The elongation is observed to be 1 mm. What will be the elongation of another steel wire of length 2L, of cross sectional area ½ A, if the tension is 2T?
SOLUTION:
Since the second wire is made of steel, Y for the second wire is the same as that for the first. That is
![]()
Solving for ![]() ,
,