USING PROPORTION

A proportion is defined as the equality of two ratios; for instance p/q = s/r is a proportion. Proportions can be used to determine the expected change in one quantity when another quantity changes. Proportion can be used in everyday life to answer questions such as whether a kilo of large potatoes is a better buy on a weight-per-unit-area basis than a kilo of small potatoes.

To illustrate the use of proportions, consider the pricing of pizza. Suppose that a small pizza costs a certain amount. How much should a larger pizza cost? If the cost depends on the amount of ingredients used, then the cost should increase in proportion to the pizza’s area, not its diameter.

where r is the radius of the pizza and k is a constant that depends on the price of ingredients per unit area. If the area of the pizza doubles, the cost should also double but k remains unchanged.

Let us rearrange the equation above so that the two variable quantities (COST and radius) are on the right side of the equation, and the constants are on the left:

This equation should apply to any size pizza. If r increases, the COST should increase in such a way that the ratio COST/r² remains constant. Thus, we can write a proportion for pizza of two different sizes ( A and B):

EXAMPLE:

A 6-inch pizza costs 30.00 Php. How much should a 14-inch pizza cost?

SOLUTION:

Substituting COST= 30.00 Php for a pizza of radius r_A = 6 in/2 = 3 in, we can use the equation above to calculate the cost of a pizza having a radius r_B = 14 inch/2 = 7 in.

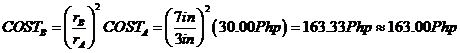
PHYSICS APPLICATION

This procedure can be used for most equations relating two quantities that change while other quantities remain constant. We simply place all the constant quantities on one side of the equation and the variables on the other side. If one variable changes, the other variable must change in a manner that keeps the variable side of the equation equal to the side with constants.

EXAMPLE 1:

The distance y that an object falls in time t if starting at rest is given by the equation . On the moon, a rock falls 10 m in 3.50 s. How much time does it take to fall 15 m, assuming that the acceleration a, is constant?

SOLUTION

We first rearrange the equation so that the constants are on one side and the variables are on the other.

If y changes, t must change so that the ratio remains constant (equal to ). Thus, for two different distances y_A and y_B, the corresponding time of fall t_A and t_B must be related by the proportion

Solving for t_B

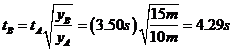
PERCENT CHANGE:

Sometimes we are told that a quantity changes by a certain percent. If a quantity increases n%, that is the same as saying that it is multiplied by a factor of 1+(n/100). If a quantity decreases n%, then it is multiplied by a factor of 1-(n/100). For example, an increase of 5 % means something is 1.05 times its original value and a decrease of 4% means it is 0.96 times the original value.

EXAMPLE 2:

A cord of wood costs 75.00Php. and has the following dimension: length L_O=8.0ft, width W_o = 4.0 ft, and height H_o = 4.0 ft. By what percent should the price of the cord be reduced if each dimension is reduced by 10%. What is the reduced price?

SOLUTION 2:

The cost C of the wood should be proportional to its volume, that is

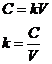
Where k is the constant that depends on the cost per unit volume and V the volume of the cord (V=LWH). Thus for two different volumes V and V₀, the corresponding costs C and C_o must be related by the proportion

Solving for C

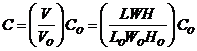
Since each dimension is 10 percent less than it should be, we substitute L= 0.90L_O, W = 0.90W_O and H = 0.90W_O to get

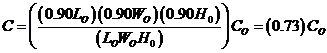
Thus, the cost should be reduced by 27 percent from the cost of the full cord, or

EXAMPLE 3:

The distance in which a car stops after the brakes are applied (the braking distance) depends on the square of the car’s speed. Suppose that the breaking distance when travelling at 18 m/s is 26 m. Calculate the breaking distance when travelling at 27 m/s. By what percent does the braking distance change if the speed of the car increases by 20 %?

SOLUTION 3:

The breaking distance is proportional to the square of the speed of the car. This tells us that

where D is the breaking distance when the speed is v. Thus for two breaking distances D_A and D_B, the corresponding speeds v_A and v_B must be related by the proportion

Solving for D_B,

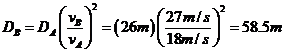
If the speed increases by 20%, then v_B=1.2v_A, the breaking distance D_B is then

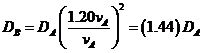
The breaking distances increases by 44%.